加速解题的高中数学公式-22利用三角关系快速解决四点公共圆问题

对于任何考试(如高考)，基础教育都有一个重要的原则：

那些在考试中得分高的人必须快速而正确地做简单的问题，以便他们有时间思考困难的问题。

因此，正确掌握一些教科书中没有提到的公式和定理，可以加快问题解决的速度，对于提高问题解决的速度，尤其是选择和填空的速度，是非常有效的。

定理22:

(1)直角三角形的顶点与斜边共面

(2)底部公共边顶角相同的三角形的所有顶点都是公共圆

接下来，我们用图像来证明和理解这个公式：

如果我们知道：C，D在线段AB的同一侧，并且

ABCD四点圆度的验证

(1)如果点d在圆o内，如下图所示

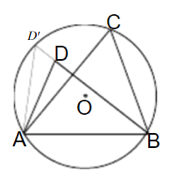
将下止点圆延伸至点D '连接上止点'。

因此，点D不能在圆o内

(2)如果点d在圆o之外，如下图所示

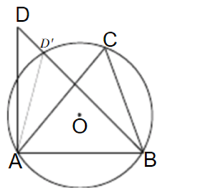
连接AD、BD。那么在点D处必须有一个线段BD与圆o相交‘以连接AD’

因此，点D不能在圆o之外。总而言之，点D必须在圆上。

记忆提示：

事实上，这是周向角的性质的应用：在同一个圆内，如果弦长相同，相应的周向角的度数相等。

通过这个简单的结论，我们可以省去一些关于四点公共圆的证明和解法的问题。这实际上是一个初中定理。然而，大多数学生在做问题时会忘记这个相对简单的定理，这是在此补充的。

接下来，我们将通过一道高考试题来展示这个公式的简单性和实用性。

例如：(2012上海)已知AB和CD是圆o的弦，AB//CD，M是AB的中点，DM与圆o和e相交，证明了EMOC的四点公共圆

答：第一步是用本质教育的第一步来翻译：把单词翻译成数字；

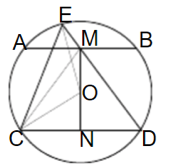
看着目标，考虑我们上面说的定理，连接运行经验，运行经验，运行经验，运行经验，运行经验，运行经验，反向扩展运行经验和运行经验的交集到N，如上图所示

所以EMOC在四点钟是圆的

如果我们很好地利用这个公式，我们可以有更多的思考路径，简化许多复杂的操作，并迅速解决答案！

定理22:

(1)直角三角形的顶点与斜边共面

(2)底部公共边顶角相同的三角形的所有顶点都是公共圆

你还记得吗？

注意(识别号：本质150)，下载此讲义