吴国平2020年的高考只剩下三个月了我该怎么办从强制考试的热点开始
吴国平:2020年的高考只剩下三个月了。我该怎么办?从强制考试的热点开始

再过三个月左右,高考将于2020年举行。剩下的时间对每个考生来说都是极其宝贵的。因此,如何利用好每一分每秒来提高复习效率,应该是考生关心的问题。像高考数学复习一样,有许多重要的、困难的和热点,但我们必须掌握一些必要的考试要点,如知识点和与立体几何有关的问题。
分析了各省市高考数学中与立体几何相关的试题类型,特别是对考试内容、考试方法和考试重点的总体评价。分析了立体几何的知识定理、技能要求、解题方法、数学思想和能力要求,总结了高考立体几何的试题分布类型和分数比例。所有这些都有助于我们提高数学成绩。
与立体几何相关的试题注重知识与能力相结合的命题理念,在试题编排上体现三个突出方面,即突出立体几何的主要基础知识、基本技能和基本思维方法的考试;突出对共性和共性的考察;突出对空间想象、推理和论证、转化和转化的考查。
事实上,无论什么样的数学知识,考生都应该学会挖掘知识之间的内在联系,不断创新,抓住关键点,从而提高复习效率。

三维几何相关高考数学试题分析,解释1:
如图所示,在金字塔p-ABCD中,底部ABCD是直角梯形,(1)求出由投影面和平面投影面形成的角度的正弦值;
(2)在边PD上有满足∠ AEC=90的点E吗?

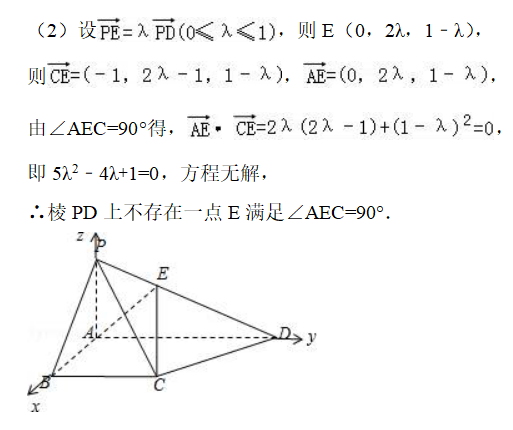
检查现场分析:
直线和平面形成的角度;垂直于平面的直线的判断。
问题分析:
(1)以A为坐标原点,建立空间直角坐标系,得到PCD与平面的法向量,这是需求;
(2)假设E满足条件,列出方程并判断方程在[0,1上是否有解]可以得出结论。

三维几何相关高考数学试题分析,解释2:
如图所示,在立方体ABCD﹣A1B1C1D1中,m、n和p分别是边AB、BC和C1D1的中点。
验证:(1)AP∑平面C1MN;
(2)平面B1BDD1⊥平面C1MN.
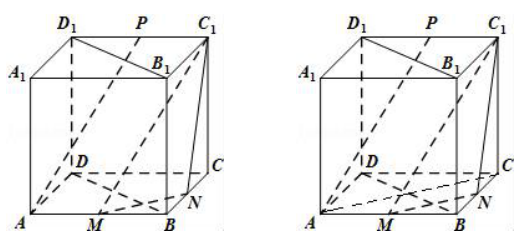
证明了:(1)在立方ABCD-A1 B1 C1 D1中,
* M、n和p分别是边AB、BC和C1D1的中点。
∴AM=PC1,
和调幅∑光盘,PC1∑光盘,所以调幅∑PC1,
∴四边形AMC1P是平行四边形,
∴AP∥C1M,
接入点平面C1MN、C1M平面C1MN、
∴AP∥飞机公司.
(2)连接交流,在AC⊥BD广场ABCD,
m和N分别是边AB和边BC的中点。
∴MN∥AC,
∴MN⊥BD,
在立方体ABCD-A1 B1 C1 D1中,DD1⊥平面ABCD,
还有mn平面ABCD,
∴DD1⊥MN,
而DD1∪DB=D,DD1,DB平面BDD1B1,
∴MN⊥飞机BDD1B1,
锰平面C1MN,
∴飞机B1BDD1⊥飞机C1MN.
检查现场分析:
垂直于平面的平面的确定;直线与平面平行度的测定。
问题分析:
(1)推导出四边形AMC1P是一个平行四边形,因此AP∑C1M可以证明AP∑平面C1MN.
(2)连接AC,推导出MN⊥BD,DD1⊥MN,从而MN⊥平面BDD1B1,从而证明平面B1BDD1⊥平面C1MN.
与立体几何相关的高考数学试题更好地处理了基础与综合、继承与创新的关系。它将立体几何与学科知识和能力结合起来。一方面,它考虑了文科和理科之间的差异,突出了动态变化。另一方面,它从不同角度诠释了教学的价值取向,形成了自己鲜明的立体几何命题风格和试题特点。
根据试题所涵盖的知识内容和解决问题所采用的思维方式,三个-
头条
图文推荐
-

高考倒计时是2个月 廉江中学举行了一次特别的高考冲刺认捐会议 誓言有助于现场直播
2020-05-07 15:26
-

居然还有书画等级考试?书画等级考试 介绍
2019-12-13 14:58
-

“你见过凌晨四点的哈佛吗?”中国学生拼起命来,连觉都不用睡
2019-12-13 14:35
-

2020届高校毕业生874万人,再创新高!就业难?这些专业已成赢家
2019-12-13 14:26




